こんにちは。今回は、数学Bの空間ベクトルで学習する四面体の体積の求め方について解説します。
四面体の体積を求める問題とは
高校数学Bの空間ベクトルでは、応用問題として四面体の体積を求める問題を扱うことがあると思います。四面体の体積を求める問題は、空間ベクトルのあらゆる知識を使うので、1問で多くのことを学ぶことができるため、空間ベクトルの総合問題(まとめ問題)の練習としては最適です。具体的には、次のような問題です。
A(0, 0, 0), B(2, 0, 0), C(1, 2, 1), D(0, 1, 2)とする。このとき、四面体ABCDの体積を求めなさい。
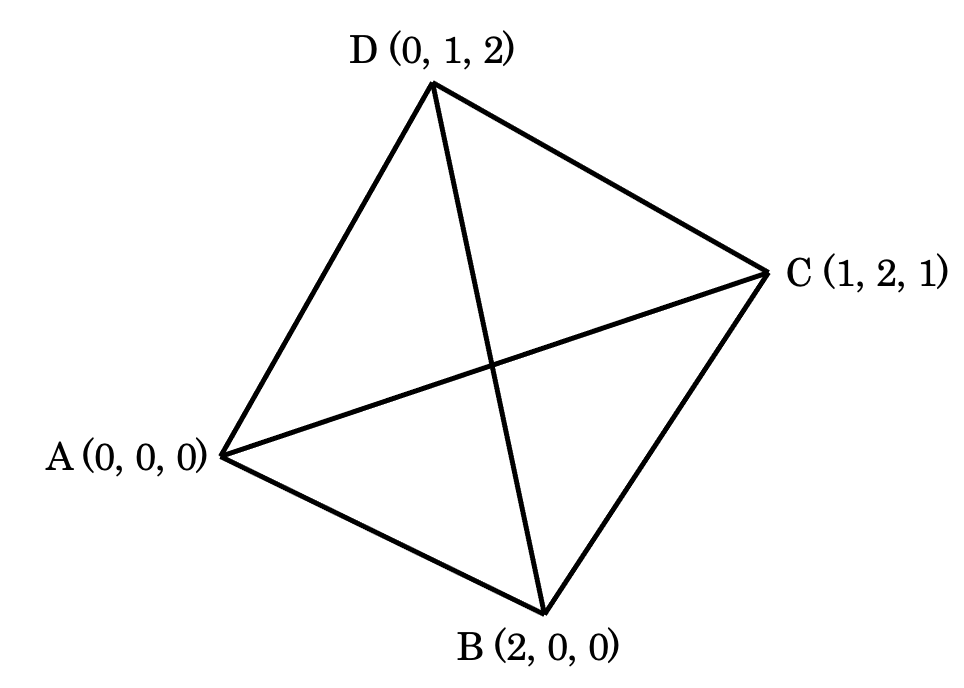
四面体の体積を求める問題とは、上の図形の体積を求めましょう、という問題になります。解説は後でやることにして、基本事項を順に確認していくことにしましょう。
四面体の体積の求め方
四面体の体積の求め方ですが、実は解法が色々とあります。今回は色々と解法があるうちの「点と平面の距離を用いて体積を求める方法」について解説していきます。
まずは、四面体の体積を求める方法の全体像を確認しましょう。
Step1:底面積を求める
4面のうち、底面を決め、まずはその底面積を求めます。例えば、四面体ABCDの体積を求める問題で、三角形ABCを底面と決めたのなら、その三角形ABCの面積を求めましょう。
Step2:底面に向かって垂線を下ろす
頂点から底面に向かって垂線を下ろしましょう。例えば、四面体ABCDの体積を求める問題で、三角形ABCを底面と決めたのなら、点Dから三角形ABCに向かって垂線を下すことになります。
Step3:高さを求める
次に高さを求めます。例えば、点Dから三角形ABCに向かって垂線を下した場合、その垂線の足をHとすると、DHが高さになりますので、DHの長さを頑張って求めることになります。
Step4:公式を用いて体積を求める
Step1〜Step3までで四面体の体積と高さを求めることができましたので、あとは体積の公式でサクッと求めて終わりになります。
このStep3の四面体の高さを点と平面の距離公式を使って求めることになります。
点と平面の距離公式
次に、点と平面の距離公式をおさらいします。具体的には次の公式になります。
点A\(x_1,y_1,z_1\)と平面\(\alpha\):\(ax+by+cz+d=0\)の距離\(d\)は
$$ d = \frac{|ax_1+by_1+cz_1+d|}{\sqrt{a^2+b^2+c^2}} $$
で求められる。
点Aと平面\(\alpha\)の距離とは,点Aから平面\(\alpha\)におろした垂線をAHとしたときの線分AHの長さ\(L\)のことです。
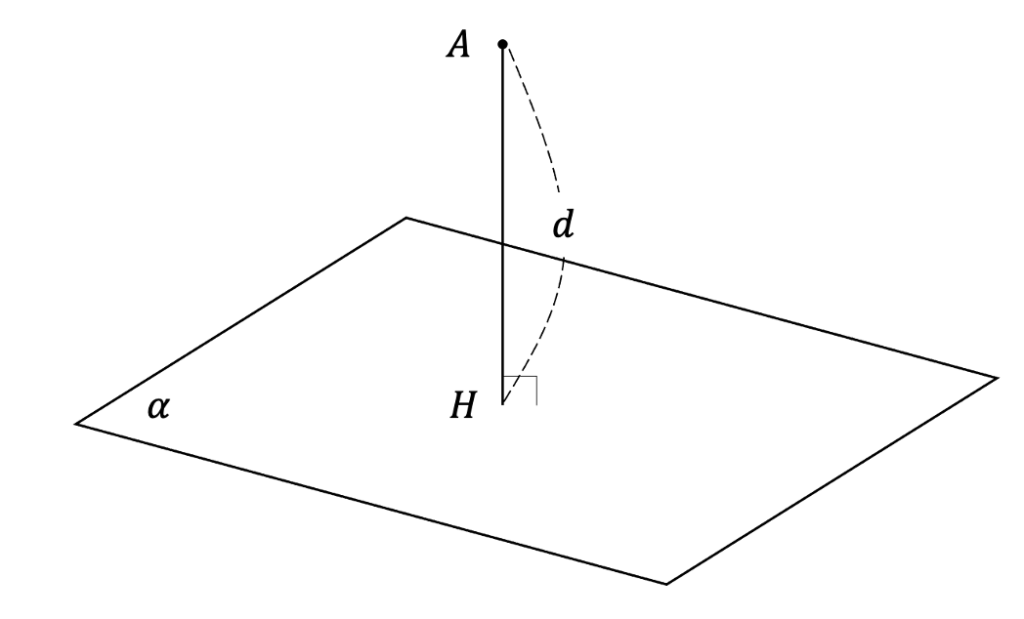
点と平面の距離公式の拡張版として覚えておくのがオススメです。点と平面の距離公式と形も似ているので、比較的覚えやすいと思います。
例題の解説
四面体の体積を求める問題は次のような例題でした。
A(0, 0, 0), B(2, 0, 0), C(1, 2, 1), D(0, 1, 2)とする。このとき、四面体ABCDの体積を求めなさい。

最初に示したStep1からStep4の手順に従って求めていくことにしましょう。
Step1:底面積を求める
まずは四面体の底面積を求めることから始めます。どの面を底面としても構いませんが、今回は三角形ABCを底面とすることにします。よって、Step1では三角形ABCの面積を求めることが目標です。
目標:A(0, 0, 0), B(2, 0, 0), C(1, 2, 1)とするとき、三角形ABCの面積を求める。
さて、空間の3点を結ぶ三角形の面積を求めることになりました。空間の3点を結ぶ三角形の面積は次の公式で求めることができます。
3点A,B,Cを頂点とする三角形ABCの面積Sは
$$ S = \displaystyle \frac{1}{2} \sqrt{|\overrightarrow{AB}|^{2}|\overrightarrow{AC}|^{2}-(\overrightarrow{AB}・\overrightarrow{AC})^2} $$
で求められる。
本問の場合、\(\overrightarrow{AB}=(2, 0, 0)\),\(\overrightarrow{AC}=(1, 2, 1)\)であるので,
$$ S = \displaystyle \frac{1}{2} \sqrt{|\overrightarrow{AB}|^{2}|\overrightarrow{AC}|^{2}-(\overrightarrow{AB}・\overrightarrow{AC})^2} = \displaystyle \frac{1}{2} \sqrt{4・6-2^2} =\sqrt{5} $$
と求められます。よって、三角形ABCの面積は\(\sqrt{5}\)となります。
Step2:垂線を下そう
次に垂線を下ろします。点Dから平面ABCに向けて垂線を下ろしましょう。

点Dから平面ABCに下ろした垂線の足を点Hとおきます。Step3では、このDHの長さを求めるのが目標になります。
Step3:DHの長さを求めよう
Step3では、四面体の高さであるDHの長さを求めます。ここで、点と平面の距離公式を使いたいのですが、平面ABCの面の方程式がわかっていないので、まずは、平面ABCの方程式を求めるところから始めます。
目標:A(0, 0, 0), B(2, 0, 0), C(1, 2, 1)とするときの平面ABCの方程式を求める
ここでは素直に平面の方程式を\(ax+by+cz+d=0\)とおいて、定数\(a,b,c,d\)を求めることにしましょう。\(ax+by+cz+d=0\)とおき、A(0, 0, 0), B(2, 0, 0), C(1, 2, 1)を代入しすれば、次の連立1次方程式が成立します。
\begin{equation} \left\{ \, \begin{aligned} & d = 0 \\ & 2a + d = 0 \\ & a+2b+c+d = 0 \end{aligned} \right. \end{equation}
これより、\(a = d = 0\)だと分かります。また、\( 2b+c=0 \)となるので、\(k\)を任意定数すれば、\(b=k\)、\(c=-2k\)となります。これらを元の平面の方程式に代入することで、求める方程式は
$$ ky-2kz = 0 $$
と求められます。つまり、
$$ y – 2z =0 $$
だと分かります。よって、\(y – 2z =0\)と点D(0,1,2)の距離は、点と平面の距離公式を用いて
$$ DH = \frac{|1-4|}{\sqrt{1^2+(-2)^2}} = \frac{3\sqrt{5}}{5} $$
と求められます。
Step4:四面体の体積を求める
Step1で底面積\(S\)は\(S=\sqrt{5}\)、Step3で高さ\(DH\)が\(DH = \displaystyle \frac{3\sqrt{5}}{5} \)だと分かりましたので、四面体の体積\(V\)は
$$ V = \frac{1}{3}S×DH = \frac{1}{3}×\sqrt{5}×\frac{3\sqrt{5}}{5} =1 $$
と求められます。よって、答えは1です。
補足:平面の方程式の求め方(外積を知っている人向け)
点と平面の距離を求める際に、平面の方程式を求めました。今回は求める方程式を\(ax+by+cz+d=0\)とおいて、連立方程式にして求めました(多分これが一番分かりやすいと思われるため)。教科書には次の平面の方程式の公式が載っていると思います。
平面の方程式
点\( A(x_0,y_0,z_0) \)を通り、\( \overrightarrow{n}=(a,b,c) \)を法線とする平面の方程式は、
$$ a(x-x_0)+b(y-y_0)+c(z-z_0)=0 $$
もちろんこれを使っても求めることができます。
目標:A(0, 0, 0), B(2, 0, 0), C(1, 2, 1)とするときの平面ABCの方程式を求める
このとき、\(\overrightarrow{AB}=(2, 0, 0)\),\(\overrightarrow{AC}=(1, 2, 1)\)なので、外積\(\overrightarrow{AB}×\overrightarrow{AC}\)は次のように求められる。
$$ \overrightarrow{AB}×\overrightarrow{AC} = (0,-2,4) $$
よって、\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)に垂直なベクトルを\(\overrightarrow{n}\)とすると、\(\overrightarrow{n} = (0,-2,4)\)となる。これより、平面ABCの方程式は、以下のように求められます1。
$$ -2(y – 0) + 4(z-0) = 0 $$
よって、
$$ y – 2z = 0 $$
となります。
まとめ
今回は、点と直線の距離を用いて四面体の体積を求める方法を解説しました。ぜひマスターしてみてください。最後までお読みいただきありがとうございました。



コメント