こんにちは。今回は、相加相乗平均を用いて最小値を求めるときに等号成立条件が必要な理由を解説していきます。
相加相乗平均について
相加相乗平均とは一般に次のような不等式を指します。
\(a>0\)、\(b>0\)のとき、次の不等式が成り立つ。
$$ \frac{a+b}{2}\geq \sqrt{ab} $$
ただし、等号成立は\(a=b\)のときである。
どの参考書にも相加相乗平均の関係では等号成立条件が書かれていると思いますし、不等式を証明するときも「等号成立を求めよ」と書かれることが多いと思います。では、なぜわざわざ等号成立条件が書かれているのでしょうか。これは、相加相乗平均で最小値を求めるときには必ず等号成立条件が必要だからです。
相加相乗平均で最小値を求めるとは
まずは基本的な話ですが、相加相乗平均で最大値・最小値を求めるとは一体どういうことなのかを解説していきます。例えば、次のような問題を見てください。
\(a\)は正の数とする。このとき、
$$ a+\frac{4}{a} $$
の最小値を求めよ。
この問題では、与えられた式に\(a\)が分子と分母の両方にあります。このような問題では、相加相乗平均を使って最小値を求めることができます。
\(a>0\)、\(\frac{4}{a}>0\)であるから、相加相乗平均の関係を用いて
$$ a+\frac{4}{a}\geq 2\sqrt{a・\frac{4}{a}}=2・2=4 $$
となるから、
$$ a+\frac{4}{a}\geq 4 $$
である。等号が成立するのは\(a=\frac{4}{a} \)のとき つまり\(a=2\)のときである。
したがって最小値は4である。
このようにして最小値を求めることができます。ここで1つ注意があって、途中の等号成立条件の確認をせずに
\(a>0\)、\(\frac{4}{a}>0\)であるから、相加相乗平均の関係を用いて
$$ a+\frac{4}{a}\geq 2\sqrt{a・\frac{4}{a}}=2・2=4 $$
となるから、
$$ a+\frac{4}{a}\geq 4 $$
したがって最小値は4である。
としてはいけません!(論理の飛躍がある)
なぜならば、等号成立条件を確認するまで最小値の存在が保証されないからです。どういうことなのか、次節で詳しく解説していきます。
等号成立条件を確認するまで最小値の存在が保証されないとは
例題1の与式を
$$ f(x)=a+\frac{4}{a} $$
とおきます。相加相乗平均を使って
$$ f(x)\geq 4 $$
という不等式を導いたわけですが、この段階では、関数\(f(x)\)が4以上である、ということを示しただけで、最小値は何も分かっていません。つまり、関数\(f(x)\)は常に4以上であるということを示しただけにすぎないのです。グラフにすると、次のようになります。
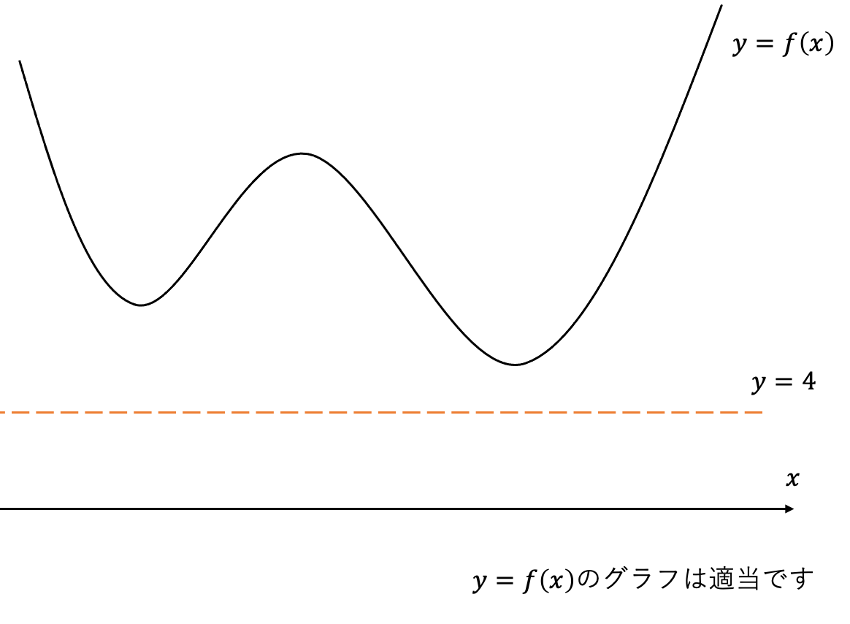
もし、関数\(f(x)\)がこのようなグラフであれば、最小値は4よりも大きくなってしまいます。
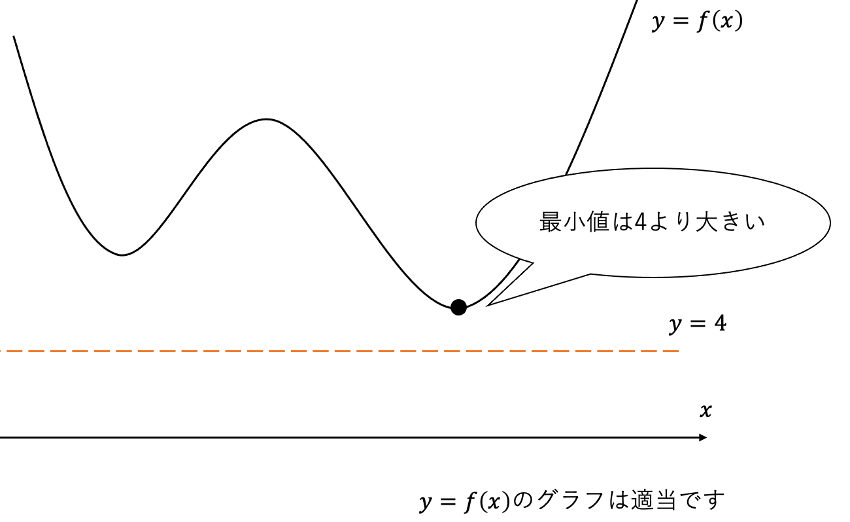
つまり、関数\(f(x)\)が4以上であるからといって、最小値は4とは限らないのです。では、次のようなグラフならどうでしょう。

このようなグラフであれば、最小値は4といえます。つまり、\(f(x)=4\)をとる\(x\)を確認できて初めて最小値が4であるといえるのです。なので、相加相乗平均から最小値を求めるときには、等号成立条件が必要なのです。ここまでの議論をまとめます。
相加相乗平均から最小値を求めるときには、等号成立条件が必要である
解答上の注意点
最後になりますが、解答上の注意点があります。
先も述べたように、\(f(x)=4\)をとる\(x\)を確認できて初めて最小値が4であるといえます。例えば、次のような回答を見かけることがありますが、等号成立条件を確認する順番がおかしいです。
\(a>0\)、\(\frac{4}{a}>0\)であるから、相加相乗平均の関係を用いて
$$ a+\frac{4}{a}\geq 2\sqrt{a・\frac{4}{a}}=2・2=4 $$
となるから、
$$ a+\frac{4}{a}\geq 4 $$
したがって最小値は4である。
なお、等号が成立するのは\(a=\frac{4}{a} \)のとき つまり\(a=2\)のときである。
この回答では、
相加相乗平均を使う→最小値を出す→等号成立条件を確認する
という順番になっていますが、これは順番がおかしいです。\(f(x)=4\)をとる\(x\)を確認できて初めて最小値が4であるといえるので、順番としては
相加相乗平均を使う→等号成立条件を確認する→最小値を出す
という順番になっていないといけません。つまり、解答にすると次のようになります。
\(a>0\)、\(\frac{4}{a}>0\)であるから、相加相乗平均の関係を用いて
$$ a+\frac{4}{a}\geq 2\sqrt{a・\frac{4}{a}}=2・2=4 $$
となるから、
$$ a+\frac{4}{a}\geq 4 $$
である。等号が成立するのは\(a=\frac{4}{a} \)のとき つまり\(a=2\)のときである。
したがって最小値は4である。
ここまでの議論をまとめておきます。
等号成立条件を確認してから最小値を出す
おわりに
相加相乗平均を用いて、最小値(最大値)を求めるときには、必ず等号成立条件を確認する必要があります。教科書や教科書傍用問題集では、相加相乗平均に関する問題は、相加相乗平均を用いて不等式を示す問題ばかり掲載されています。そのため、入試問題演習を始めてようやく最小値を求める問題に出会うため、このような誤謬がよく起きているのだと思います。入試問題では、相加相乗平均を用いて、最小値(最大値)を求める問題がよく出題されています。皆さんは気をつけてください。
最後になりますが、このような議論はコーシー・シュワルツの不等式を用いた最小値(最大値)を求める問題においても全く同じことがいえます。コーシー・シュワルツの不等式を使う際にも、等号成立条件の確認を忘れないようにしましょう。
最後までお読みいただき、ありがとうございました。



コメント