完全順列とは何か？完全順列の漸化式の求め方とその一般項、その極限も解説！

今回は、入試でよく出題される完全順列について解説していきます。完全順列は入試でも頻出のテーマで、過去には共通テストや2次試験で出題されています。なので、勉強していて損はないと思います。

完全順列とは
完全順列の演習問題①（具体的に書き出す）
1. 演習1：具体的に書き出す
完全順列の演習問題②（漸化式を求める）
1. 例題2：漸化式を求める
2. 漸化式を使ってnが5以上の場合も求めてみる
完全順列の一般項
完全順列の一般項の極限
おわりに

完全順列とは

完全順列とは、別名、かく乱順列やモンモール数とも呼ばれ、1，2，…，$n$を並び替えてできる順列のうち、$i$番目が$i$でないものを満たす順列のことです。

完全順列とは

1，2，…，$n$を並び替えてできる順列のうち、$i$番目が$i$でないものを満たす順列のこと

これだけではよくわからないと思うので、実際に例を見てみることにしましょう。

例：プレゼント交換の順列

完全順列はよくプレゼント交換会で例えられることが多いです。具体的には次のようなケースです。例えば、あなたとあなたの友達3人の合計4人でプレゼント交換会をすることになりました。ただし、ここで誰が誰のプレゼントをもらうかは完全にランダムで決めるものとします。このとき、どのプレゼントが自分の元にやってくるかはランダムなので、プレゼント交換で自分のプレゼントが戻ってきてしまう可能性もあるわけです。でも、自分のプレゼントが戻ってきたら悲しいですよね。4人全員が誰も自分のプレゼントを受け取らずに、他の人のプレゼントを受け取る場合の数を考えるのが、完全順列になります。

この問題の解答は後で考えることにします。

なお、例として4人の場合を考えましたが、2人でも3人でも5人でも$n$人でも同様に考えます。

完全順列の求め方

次に、実際に完全順列の求め方を解説していきます。基本的には、次のような方針で解きます。

完全順列の求め方

① $n$が4〜5程度までの具体的な数のとき
実際に全てのパターンを書き出して、求める。（このとき、樹形図を活用するとよい）

② $n$が大きいときや文字のとき
一般項を求める。

この記事では、①の具体的な数の場合を「プレゼント交換の例」と「演習1」で、②の一般項を求める場合を「例題1」でやることにします。

プレゼント交換の解答

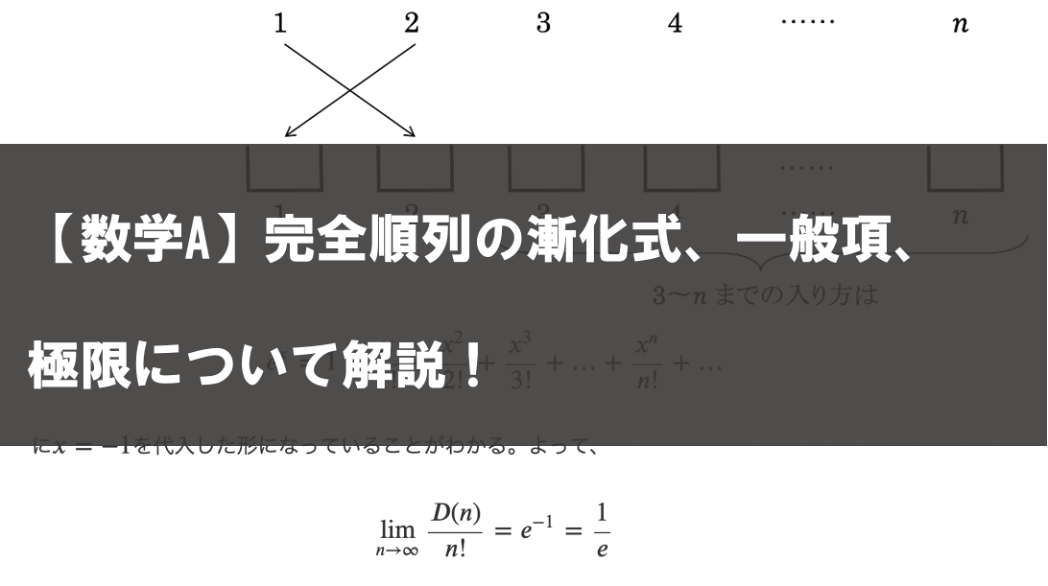
さて、ここで、例として扱った4人のプレゼント交換会の例の解答を考えてみることにします。プレゼントとヒトに1〜4までの番号を振って考えることにします。

人と同じ番号の書かれているプレゼントがその人の持ってきたプレゼントです。さて、ここで、考えやすくするために、人の直上にきたプレゼントをその人は受け取ることにします。

例えば、例1のようにプレゼントが次のように並べば、4人全員が自分の持ってきたプレゼントを受け取らずに友達の持ってきたプレゼントを受け取ることができます。

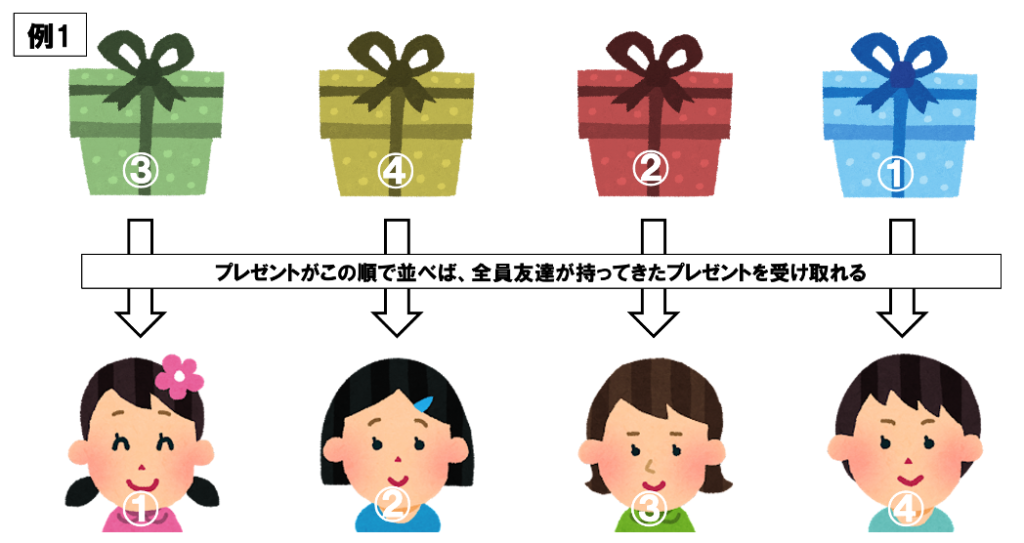
しかし、例えば、例2のようにプレゼントが並べば、②番の人は自分の持ってきたプレゼントを受け取ることになってしまい、完全順列でなくなってしまいます。

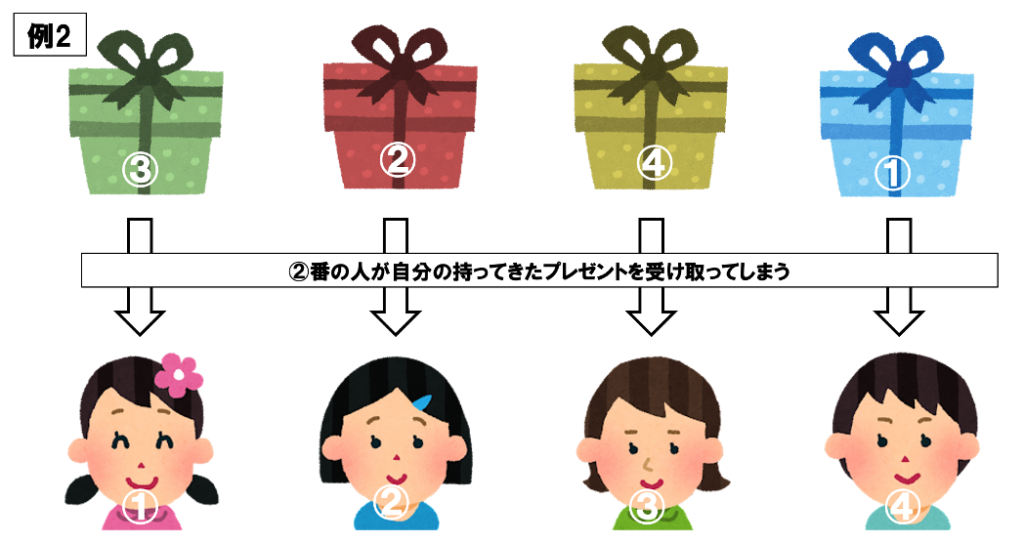
つまり、1番目に①と書かれたプレゼントが置かれず、2番目に②と書かれたプレゼントが置かれず、3番目に③と書かれたプレゼントが置かれず、4番目に④と書かれたプレゼントが置かれないとき、4人全員が友達の持ってきたプレゼントを受け取ることができます。

ポイント

1番目に①と書かれたプレゼントが置かれず、2番目に②と書かれたプレゼントが置かれず、3番目に③と書かれたプレゼントが置かれず、4番目に④と書かれたプレゼントが置かれないとき、4人全員が友達の持ってきたプレゼントを受け取ることができる！

ここからは、1番目が1ではなく、2番目が2ではなく、3番目が3ではなく、4番目が4ではない順列を考えていきます。これを考えるには、実際に全てのパターンを書き出すとよいです。樹形図を用いて順番に書き出してみることにします。

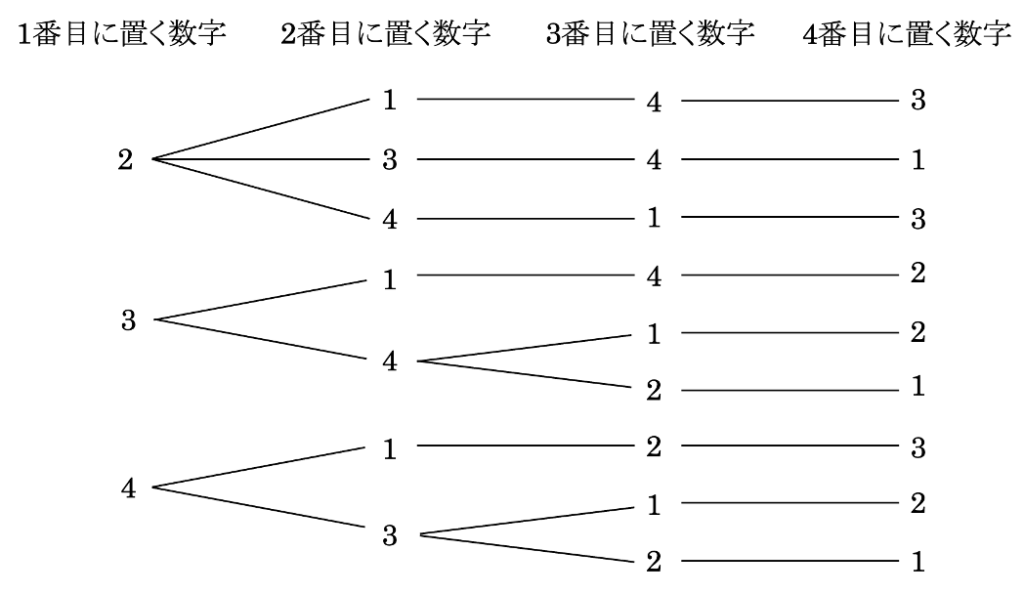
よって、9通りと分かります。4個のものの並べ方は$4!=24$通りなので、完全にランダムに交換した場合、9/24で4人誰も自分の持ってきたプレゼントを受け取らずに済むということです。逆に、15/24で誰か1人以上は自分の持ってきたプレゼントを受け取ってしまうということになります。

まとめ

$n=4$の場合、4人誰も自分の持ってきたプレゼントを受け取らずに友達の持ってきたプレゼントをもらう確率は次のようになる。

$$ \displaystyle \frac{9}{4!} = \frac{9}{24} \simeq 38 [\%] $$

最初、私はこれを知ったとき、38%か〜、意外と低いなと思いました。

なお、今回、例で扱った$n=4$のときは、特に大学入試頻出ですので、必ずできるようにしておきましょう。以下の演習問題でもう一度再確認しましょう。

完全順列の演習問題①（具体的に書き出す）

完全順列のうち、具体的に書き出す問題を演習しましょう。

演習1：具体的に書き出す

演習1

場所1から場所$n$に異なる$n$個のものが並んでいる。これらを並び替えてどれもがもとの位置にならないようにする方法の総数を$D(n)$とする。ただし、$n\geq 2$とする。
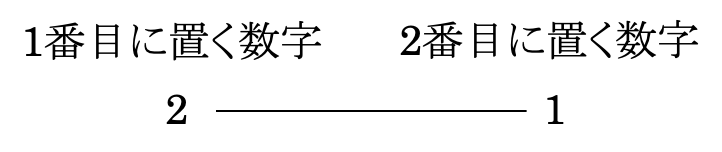
（1）$D(2)$を求めよ。
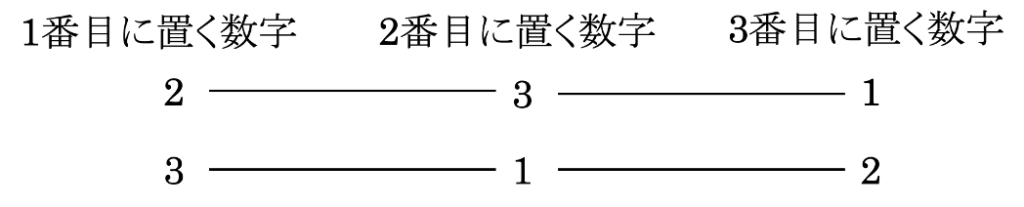
（2）$D(3)$を求めよ。
（3）$D(4)$を求めよ。

（（3）2004年東工大）

（3）は2004年の東工大後期の問題です。具体的に数を書き出して求めてみましょう。

演習1の答え

（1）$n=2$のとき、並べ方は以下のようになる。

よって、$D(2)=1$である。

（2）$n=3$のとき、並べ方は以下のようになる。

よって、$D(3)=2$である。

（3）$n=4$のとき、並べ方は以下のようになる。

よって、$D(4)=9$である。

なお、樹形図を使わず、次のように書き出しても良いと思います。

（1）$n=2$のとき、並べ方は以下のようになる。
$(2, 1)$
よって、$D(2)=1$である。

（2）$n=3$のとき、並べ方は以下のようになる。
$(2, 3, 1), (3, 1, 2)$
よって、$D(3)=2$である。

（3）$n=4$のとき、並べ方は以下のようになる。
$(2, 1, 4, 3), (2, 3, 4, 1), (2, 4, 1, 3), $
$(3, 1, 4, 2), (3, 4, 1, 2), (3, 4, 2, 1), $
$(4, 1, 2, 3), (4, 3, 1, 2), (4, 3, 2, 1), $
よって、$D(4)=9$である。

完全順列の演習問題②（漸化式を求める）

次に、完全順列の一般項について考えることにします。$n$が大きい時や、文字のときは漸化式から求めます。

例題2：漸化式を求める

次に、完全順列の漸化式を求めてみましょう。次の例題1は演習1の続きです。

例題1

場所1から場所$n$に異なる$n$個のものが並んでいる。これらを並び替えてどれもがもとの位置にならないようにする方法の総数を$D(n)$とする。ただし、$n\geq 2$とする。
$n\geq 4$に対して、$D(n)=(n-1) \{ D(n-2)+D(n-1) \} $を証明せよ。

（2004年東工大）

方針：ここでは考えやすくするために、1〜$n$までの数字を1〜$n$まで書かれた箱に入れることを考えます。

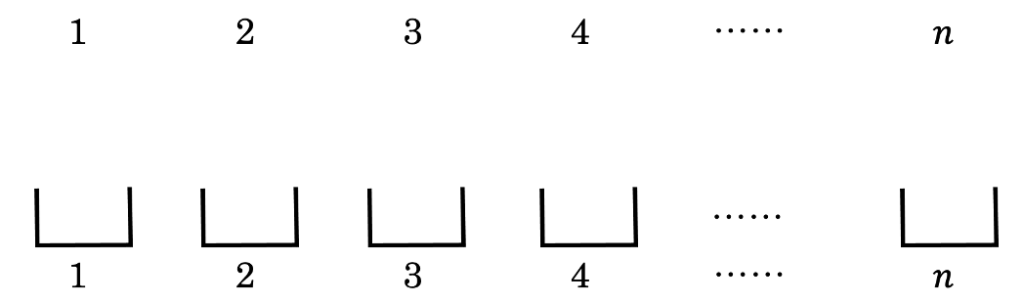
ここで、数字の箱への入れ方について次の2つの場合が考えられます。
（イ）入れられたら入れ返すとき
（ロ）入れられても入れ返さないとき
それぞれの場合について考えてみます。

（イ）入れられたら入れ返すとき
入れられたら入れ返すときというのは、ある数字が箱に入った時にその数字の箱に入り返すという意味です。例えば、1が2の箱に入れられたときは、2が1の箱に入るときということになります。

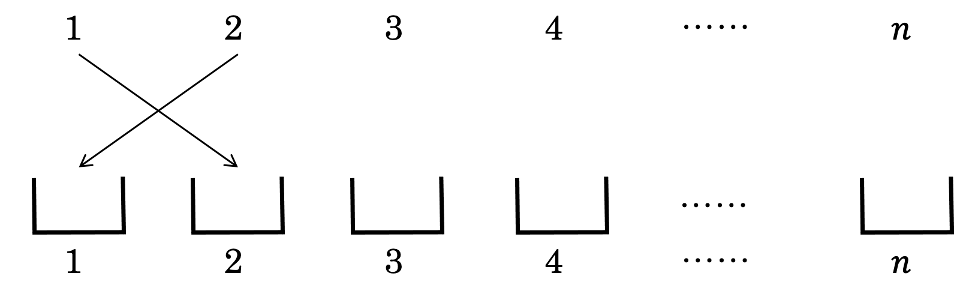
このとき、残った3〜$n$までの入り方の総数は$D(n-2)$通りになります。

1は入ることのできる箱が2から$n$まであるので、（イ）の場合の全ての総数は$(n-1)D(n-2)$通りになります。

（ロ）入れられても入れ返さないとき
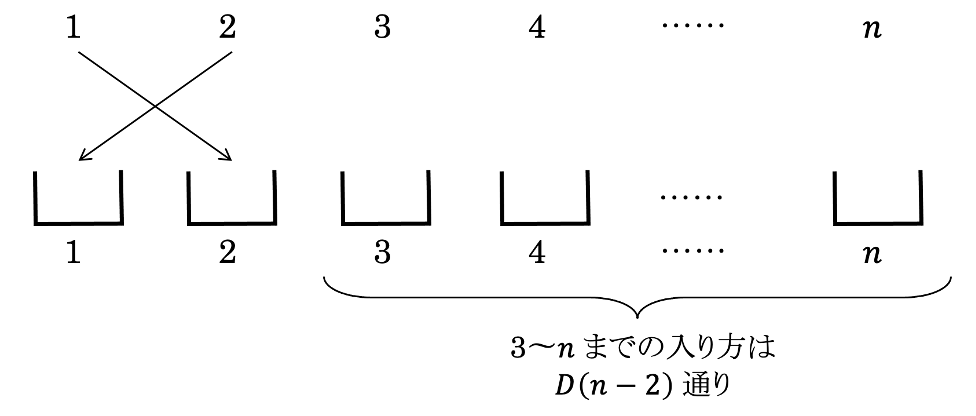
入れられても入れ返さないときというのは、（イ）以外の場合です。例えば、1が2の箱に入れられたとき、2は1の箱には入らずに別の箱に入るということです。

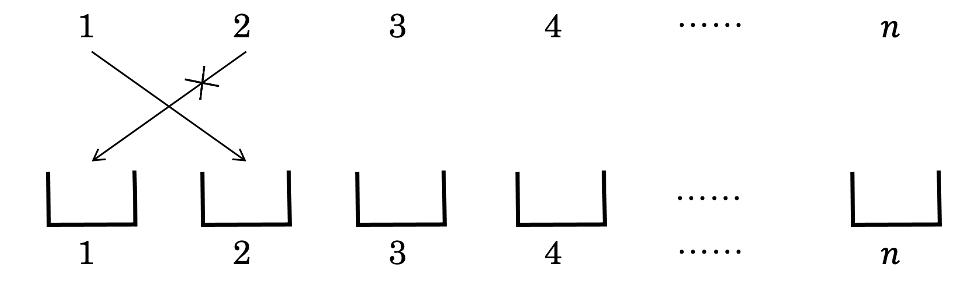
このとき、2から$n$までが箱に入る総数は$D(n-1)$通りあります。1が入ることのできる箱は2から$n$まであるので、（ロ）の場合の全ての総数は$(n-1)D(n-1)$通りになります。

このことを解答には書けばOKです。少し前置きが長くなりましたが、解答1に入ります。

解答1

1，2，3，…，$n$までの数字を1，2，3，…，$n$までの箱に入れる入れ方を考える。数字が箱に入るとき、数字の入れ方を考えることにより、次の2つの場合が考えられる。
（イ）入れられたら入れ返すとき
（ロ）入れられても入れ返さないとき

（イ）のとき、まず、1を2の箱に入れるときを考える。3，4，5，…，$n$の$n-2$個の数字を3，4，5，…，$n$の$n-2$個の箱に入れる入れ方は、$D(n-2)$通り。1は入ることのできる箱が2から$n$の$n-1$通りあるので、（イ）の場合の全ての入れ方は$(n-1)D(n-2)$通りである。

（ロ）のとき、まず、1を2の箱以外に入れるときを考える。2，3，4，…，$n$の$n-1$個の数字を2，3，4，…，$n$の$n-1$個の箱に入れる入れ方は$D(n-1)$通り。1が入ることのできる箱は2から$n$の$n-1$通りあるので、（ロ）の場合の全ての入れ方は$(n-1)D(n-1)$通りである。

以上、（イ）（ロ）より
$D(n)=(n-1) \{ D(n-2)+D(n-1) \} $

漸化式を使ってnが5以上の場合も求めてみる

通常、$n\geq 5$の場合は樹形図で書き出すのが大変なので、書き出して求めることはあまりありません。しかし、例題1で証明した漸化式を使うことにより、$n\geq 5$の場合も求めることができます。

演習1により、すでに$D(2)=1，D(3)=2，D(4)=9$であることは求められています。さて、$n=5$の場合も求めてみましょう。例題1の漸化式より、

$$ D(5)=4 \{ D(3)+D(4) \} = 4 \{ 2+9 \} = 44 $$

と求めることができます。同様に、

$$ D(6)=5 \{ D(4)+D(5) \} = 5 \{ 9+44 \} = 265 $$

などと求めることができます。

完全順列の一般項

さて、東工大の問題は、漸化式を求めて終わりでしたが、一歩進んで、完全順列の一般項も求めてみることにしましょう。例題1で求めた完全順列の漸化式

$$ D(n)=(n-1)\{D(n-2)+D(n-1)\} $$

を変形して

$$ D(n) – n D(n-1) = -\{D(n-1)+(n-1) D(n-2)\} $$

とします。

数列 $ \{D(n) – n D(n-1) \} $は、公比 $ -1 $、初項 $ D(2) – 2 D(1)=1-2・0=1 $の等比数列であるから、

$$ D(n) – n D(n-1)=1・(-1)^{n-2}=(-1)^n $$

となります。辺々$ n! $で割ると、

$$ \frac{D(n)}{n!} – \frac{D(n-1)}{(n-1)!} = \frac {(-1)^n}{n!} $$

となります。よって、$D(1)=0$とすると$ n\geq 2 $のとき

$$ \frac{D(n)}{n!} = \frac{D(1)}{1!} + \displaystyle \sum_{k=2}^{n} \frac{(-1)^k}{k!} = \displaystyle \sum_{k=2}^{n} \frac{(-1)^k}{k!} $$

となります。よって、$D(n)$は

$$ D(n) = n! \displaystyle \sum_{k=2}^{n} \frac{(-1)^k}{k!} $$

となります。以上より、完全順列の一般項を求めることができました。

完全順列の一般項

1から$ n $を一列に並べたものを $ a_1 a_2 a_3 … a_n $ とする。このとき、 $ a_i ≠ i $ （$ i=1，2，…，n $となる並べ方は

$$ n! \displaystyle \sum_{k=2}^{n} \frac{(-1)^k}{k!} $$

である。

完全順列の一般項の極限

この先は高校数学範囲外で、大学数学の範囲になるのですが、完全順列の極限は、自然対数の底（ネイピア数）と密接な関係があります。前節の完全順列の一般項を求める手順の最終行から1つ前の式から

$$ \frac{D(n)}{n!} = \displaystyle \sum_{k=2}^{n} \frac{(-1)^k}{k!} $$

であることがわかると思います。実際に、右辺を展開してみると、

$$ \frac{D(n)}{n!} = \displaystyle \sum_{k=2}^{n} \frac{(-1)^k}{k!} = \frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}-…+\frac{(-1)^n}{n!} $$

となります。この両辺に$\displaystyle \frac{1}{0!}-\frac{1}{1!}(=0)$を加えると、

$$ \frac{D(n)}{n!} = \frac{1}{0!}-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}-…+\frac{(-1)^n}{n!} $$

となります。右辺は$e^x$のテイラー展開（マクローリン展開）

$$ e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+…+\frac{x^n}{n!}+… $$

に$x=-1$を代入した形になっていることがわかる。よって、

$$ \lim_{n \to \infty}\frac{D(n)}{n!} = e^{-1} =\frac{1}{e} $$

となることが分かります。つまり、かなり大人数でプレゼント交換を行なった場合、$\displaystyle \frac{1}{e}\simeq 37 [\%]$で参加者全員が自分のプレゼントを受け取らないということになります。逆に、$63 [\%]$で参加者の誰かは自分のプレゼントを受け取ることになります。

まとめ

大人数でプレゼント交換を行なった場合、$63 [\%]$で誰かは自分のプレゼントを受け取ることになる。

今回は、プレゼント交換の例で説明しましたが、他にも、完全順列は「席替え」や「フルーツバスケット」の例などで説明されることもあります。